题目简介:
一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动,你能任意交换两列或是两行的位置。
返回 将这个矩阵变为 “棋盘” 所需的最小移动次数 。如果不存在可行的变换,输出 -1。
“棋盘” 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。
示例 1:
1
2
3
4
5
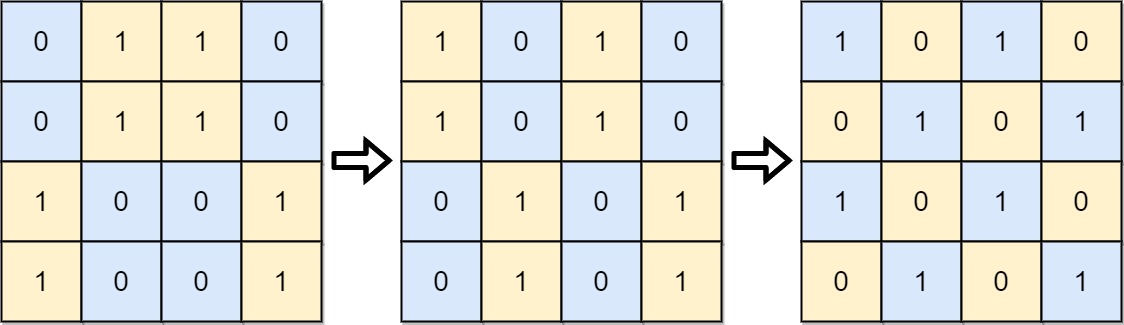
| 输入: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
输出: 2
解释:一种可行的变换方式如下,从左到右:
第一次移动交换了第一列和第二列。
第二次移动交换了第二行和第三行。
|
示例 2:
1
2
3
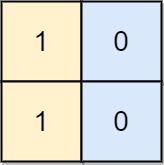
| 输入: board = [[1, 0], [1, 0]]
输出: -1
解释: 任意的变换都不能使这个输入变为合法的棋盘。
|
提示:
n == board.lengthn == board[i].length2 <= n <= 30board[i][j] 将只包含 0 或 1
思路:
看了题解勉强能看懂的一道题。
首先我们根据示例1的初始棋盘可以看出,行与列都只有两种情况,并且两种情况是完全相反的状态。
那么,我们可以归纳出,从左上角顶点出发的任意一个矩阵,只有四个顶点异或结果为0时(即都为1或都为0,或两个为1两个为0),才有可能恢复成棋盘。
并且,我们可以发现,首行和首列1的数量必须为n / 2或者为(n + 1) / 2,否则无法恢复成棋盘。
接下来说明的是如何获取最小的步数。
我们可以发现,交换行或者交换列,一次交换会形成两个错位,所以最后行的错位和列的错位必须为偶数才行。
方便起见,我们先与首行是10101...这样的棋盘进行比对错位。若当前首行为10001时,错位为1个,而n - 1 = 4才为偶数,此时比对的棋盘便是01010。
因此,当rowdiff, coldiff为奇数且n也为奇数时,需要将其变为n - rowdiff, n - coldiff。
当n为偶数时,便没有这种问题,rowdiff与n - rowdiff都为偶数,我们只需要选择最小值即可。
最后,(rowdiff + coldiff) / 2便是最后交换的次数(一次交换有两个错位)。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| class Solution {
public:
int movesToChessboard(vector<vector<int>>& board) {
int n = board.size();
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(board[0][0] ^ board[0][j] ^ board[i][0] ^ board[i][j] != 0)
return -1;
}
}
int row_sum = 0;
int col_sum = 0;
int row_diff = 0;
int col_diff = 0;
for(int i = 0; i < board.size(); i++){
row_sum += board[0][i];
col_sum += board[i][0];
row_diff += (board[0][i] == i % 2);
col_diff += (board[i][0] == i % 2);
}
if(row_sum != n / 2 && row_sum != (n + 1) / 2)
return -1;
if(col_sum != n / 2 && col_sum != (n + 1) / 2)
return -1;
if(n % 2 == 1){
if(row_diff % 2 == 1)
row_diff = n - row_diff;
if(col_diff % 2 == 1)
col_diff = n - col_diff;
}
else{
row_diff = min(row_diff, n - row_diff);
col_diff = min(col_diff, n - col_diff);
}
return (row_diff + col_diff) / 2;
}
};
|

