题目简介:
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
示例 1:
1
2
3
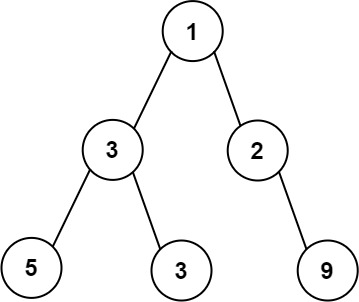
| 输入:root = [1,3,2,5,3,null,9]
输出:4
解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。
|
提示:
- 树中节点的数目范围是
[1, 3000]
-100 <= Node.val <= 100
思路:
利用广度优先遍历搜索树,小技巧是将元素压入队列的时候需要将结点的索引一同压入。
当前结点的左结点索引为index * 2,右结点为index * 2 + 1。
每一层的宽度即为队列的首尾元素索引之差,取各层的最大值即可。
tip:
- 需要用
long long来存储,否则会溢出范围。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
unsigned long long res = 0;
queue<pair<TreeNode*, unsigned long long>> qu;
qu.push(make_pair(root, 1));
while(!qu.empty()){
res = max(res, qu.back().second - qu.front().second + 1);
int now_size = qu.size();
for(int i = 0; i < now_size; i++){
auto node = qu.front();
qu.pop();
if(node.first -> left)
qu.push(make_pair(node.first -> left, node.second * 2));
if(node.first -> right)
qu.push(make_pair(node.first -> right, node.second * 2 + 1));
}
}
return res;
}
};
|
