题目简介:
给定一个二叉树的 root ,返回 最长的路径的长度 ,这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。
两个节点之间的路径长度 由它们之间的边数表示。
示例 1:
1
2
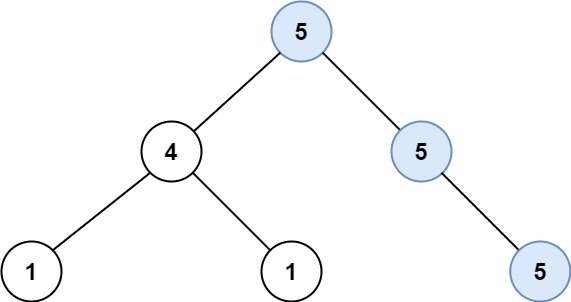
| 输入:root = [5,4,5,1,1,5]
输出:2
|
示例 2:
1
2
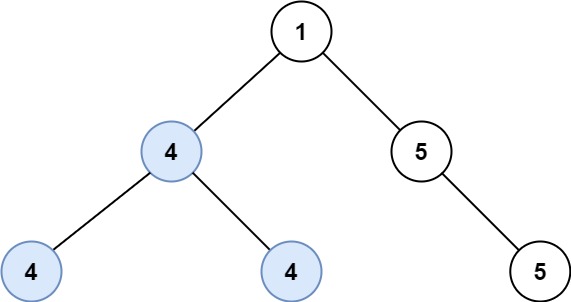
| 输入:root = [1,4,5,4,4,5]
输出:2
|
提示:
- 树的节点数的范围是
[0, 10^4]
-1000 <= Node.val <= 1000- 树的深度将不超过
1000
思路:
利用深度优先搜索,最长同值路径长度必定为某一节点的左最长同值路径长度与右最长同值路径长度之和。
我们先分别获取当前结点的左最长同值有向路径长度与右最长同值路径长度left, right。若当前结点与左结点值相同。则res_left = left + 1,否则res_left = 0;右节点也是如此。
所以最后当前结点的最长同值路径长度为res_left + res_right。
返回上一层时,返回的最长同值路径长度则为max(res_left, res_right)。(一条路到了岔路口,只能选一个方向,所以取左右两边最长的一边)
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public:
int res = 0;
int dfs(TreeNode* root){
if(!root)
return 0;
int left = dfs(root -> left);
int right = dfs(root -> right);
int res_left = 0;
if(root -> left && root -> left -> val == root -> val)
res_left = 1 + left;
int res_right = 0;
if(root -> right && root -> right -> val == root -> val)
res_right = 1 + right;
res = max(res, res_left + res_right);
return max(res_left, res_right);
}
int longestUnivaluePath(TreeNode* root) {
int temp = dfs(root);
return res;
}
};
|

