题目简介:
在一个 n x n 的矩阵 grid 中,除了在数组 mines 中给出的元素为 0,其他每个元素都为 1。mines[i] = [xi, yi]表示 grid[xi][yi] == 0
返回 grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志,则返回 0 。
一个 k 阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1 ,以及4个从中心向上、向下、向左、向右延伸,长度为 k-1,由 1 组成的臂。注意,只有加号标志的所有网格要求为 1 ,别的网格可能为 0 也可能为 1 。
示例 1:
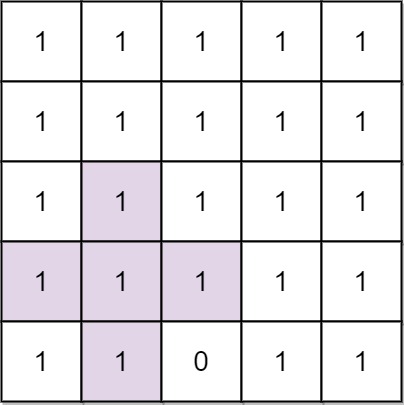
1
2
3
| 输入: n = 5, mines = [[4, 2]]
输出: 2
解释: 在上面的网格中,最大加号标志的阶只能是2。一个标志已在图中标出。
|
提示:
1 <= n <= 5001 <= mines.length <= 50000 <= xi, yi < n- 每一对
(xi, yi) 都 不重复
思路:
动态规划,以每个点为中心,从上左下右四个方向延伸,四个方向中最短的路径长度(即最少的1)则为该点的阶。
将所有点遍历完成后,返回最大值即可。
tip:
- 利用
dp[i][j][0...3]来表示四个方向的dp数组
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| class Solution {
public:
int orderOfLargestPlusSign(int n, vector<vector<int>>& mines) {
vector<vector<int>> grid(n, vector<int>(n, 1));
for(auto& item : mines)
grid[item[0]][item[1]] = 0;
vector<vector<vector<int>>> dp(n, vector<vector<int>>(n,
vector<int>(4)));
int res = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(j == 0)
dp[i][j][0] = (grid[i][j] == 1) ? 1 : 0;
else if(grid[i][j] == 1)
dp[i][j][0] = 1 + dp[i][j - 1][0];
}
for(int j = n - 1; j >= 0; j--){
if(j == n - 1)
dp[i][j][1] = (grid[i][j] == 1) ? 1 : 0;
else if(grid[i][j] == 1)
dp[i][j][1] = 1 + dp[i][j + 1][1];
}
}
for(int j = 0; j < n; j++){
for(int i = n - 1; i >= 0; i--){
if(i == n - 1)
dp[i][j][2] = (grid[i][j] == 1) ? 1 : 0;
else if(grid[i][j] == 1)
dp[i][j][2] = 1 + dp[i + 1][j][2];
}
for(int i = 0; i < n; i++){
if(i == 0)
dp[i][j][3] = (grid[i][j] == 1) ? 1 : 0;
else if(grid[i][j] == 1)
dp[i][j][3] = 1 + dp[i - 1][j][3];
res = max(res, min(min(min(dp[i][j][0], dp[i][j][1]), dp[i][j][2]),
dp[i][j][3]));
}
}
return res;
}
};
|
