题目简介:
有一个具有 n 个顶点的 双向 图,其中每个顶点标记从 0 到 n - 1(包含 0 和 n - 1)。图中的边用一个二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接,并且没有顶点存在与自身相连的边。
请你确定是否存在从顶点 source 开始,到顶点 destination 结束的 有效路径 。
给你数组 edges 和整数 n、source 和 destination,如果从 source 到 destination 存在 有效路径 ,则返回 true,否则返回 false 。
示例 1:
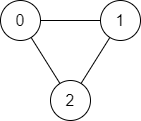
1 | 输入:n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2 |
提示:
1 <= n <= 2 * 10^50 <= edges.length <= 2 * 10^5edges[i].length == 20 <= ui, vi <= n - 1ui != vi0 <= source, destination <= n - 1- 不存在重复边
- 不存在指向顶点自身的边
思路:
首先根据edges构造图,然后进行深度优先搜索。
为了避免超时,设置两个策略:
- 利用
flag数组避免重复对一个顶点进行遍历 - 在进行构造图时,只
push_back存在的边即可。
代码如下:
1 | class Solution { |