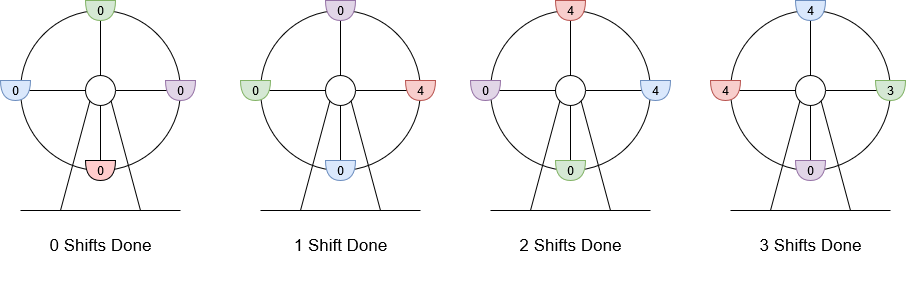
题目简介: 你正在经营一座摩天轮,该摩天轮共有 4 个座舱 ,每个座舱 最多可以容纳 4 位游客 。你可以 逆时针 轮转座舱,但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。
给你一个长度为 n 的数组 customers , customers[i] 是在第 i 次轮转(下标从 0 开始)之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ,一旦该座舱再次抵达地面,他们就会离开座舱结束游玩。
你可以随时停下摩天轮,即便是 在服务所有游客之前 。如果你决定停止运营摩天轮,为了保证所有游客安全着陆,将免费进行所有后续轮转 。注意,如果有超过 4 位游客在等摩天轮,那么只有 4 位游客可以登上摩天轮,其余的需要等待 下一次轮转 。
返回最大化利润所需执行的 最小轮转次数 。 如果不存在利润为正的方案,则返回 -1 。
示例 1:
1 2 3 4 5 6 7 输入:customers = [8,3], boardingCost = 5, runningCost = 6 输出:3 解释:座舱上标注的数字是该座舱的当前游客数。 1. 8 位游客抵达,4 位登舱,4 位等待下一舱,摩天轮轮转。当前利润为 4 * $5 - 1 * $6 = $14 。 2. 3 位游客抵达,4 位在等待的游客登舱,其他 3 位等待,摩天轮轮转。当前利润为 8 * $5 - 2 * $6 = $28 。 3. 最后 3 位游客登舱,摩天轮轮转。当前利润为 11 * $5 - 3 * $6 = $37 。 轮转 3 次得到最大利润,最大利润为 $37 。
提示:
n == customers.length1 <= n <= 10^50 <= customers[i] <= 501 <= boardingCost, runningCost <= 100
思路: 模拟,记录每次转动后的收益是否比上次高,从而保存最高收益以及当时的转动次数。
代码如下: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class Solution {public : int minOperationsMaxProfit (vector <int >& customers, int boardingCost, int runningCost) int customer_num = 0 ; int operation = 0 ; int Maxprorit = 0 ; int Totalprofit = 0 ; int res = -1 ; int now_cus = 0 ; for (int i = 0 ; i < customers.size(); i++){ operation++; customer_num += customers[i]; now_cus = min(customer_num, 4 ); customer_num -= now_cus; Totalprofit += boardingCost * now_cus - runningCost; if (Totalprofit > Maxprorit){ Maxprorit = Totalprofit; res = operation; } } if (customer_num == 0 ) return res; while (customer_num > 0 ){ operation++; now_cus = min(customer_num, 4 ); customer_num -= now_cus; Totalprofit += boardingCost * now_cus - runningCost; if (Totalprofit > Maxprorit){ Maxprorit = Totalprofit; res = operation; } } return res; } };