题目简介:
给定二叉树的根节点 root,找出存在于 不同 节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
示例 1:
1
2
3
4
5
6
7
8
9
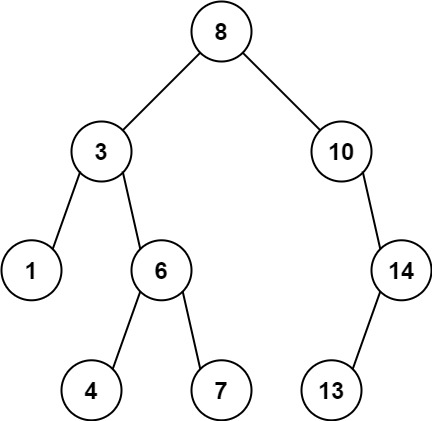
| 输入:root = [8,3,10,1,6,null,14,null,null,4,7,13]
输出:7
解释:
我们有大量的节点与其祖先的差值,其中一些如下:
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
在所有可能的差值中,最大值 7 由 |8 - 1| = 7 得出。
|
提示:
- 树中的节点数在
2 到 5000 之间。
0 <= Node.val <= 10^5
思路:
深搜,过程中保存遍历到的最大值和最小值。
当遇到叶子结点时,则更新当前遍历到的差值。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
public:
int res = 0;
void solve(TreeNode* root, int val_max_before, int val_min_before){
if(!root){
res = max(res, abs(val_max_before - val_min_before));
return;
}
val_max_before = max(val_max_before, root -> val);
val_min_before = min(val_min_before, root -> val);
solve(root -> left, val_max_before, val_min_before);
solve(root -> right, val_max_before, val_min_before);
}
int maxAncestorDiff(TreeNode* root) {
solve(root, root -> val, root -> val);
return res;
}
};
|
