题目简介:
给定一个数组 books ,其中 books[i] = [thicknessi, heighti] 表示第 i 本书的厚度和高度。你也会得到一个整数 shelfWidth 。
按顺序 将这些书摆放到总宽度为 shelfWidth 的书架上。
先选几本书放在书架上(它们的厚度之和小于等于书架的宽度 shelfWidth ),然后再建一层书架。重复这个过程,直到把所有的书都放在书架上。
需要注意的是,在上述过程的每个步骤中,摆放书的顺序与你整理好的顺序相同。
- 例如,如果这里有 5 本书,那么可能的一种摆放情况是:第一和第二本书放在第一层书架上,第三本书放在第二层书架上,第四和第五本书放在最后一层书架上。
每一层所摆放的书的最大高度就是这一层书架的层高,书架整体的高度为各层高之和。
以这种方式布置书架,返回书架整体可能的最小高度。
示例 1:
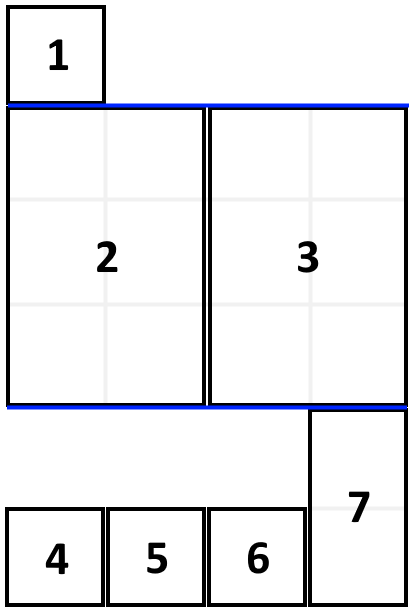
1 | 输入:books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4 |
提示:
1 <= books.length <= 10001 <= thicknessi <= shelfWidth <= 10001 <= heighti <= 1000
思路:
动态规划,dp[i]代表前i本书的最小高度,i $\in$ [1, n], n = books.size()
分为两种情况:
- 第i本书
books[i]单独为一层,则dp[i] = dp[i - 1] + books[i][1]。 - 第i本书可以和前面的几本书共处一层,则从后往前遍历,若累加的厚度
> shelfWidth,则说明放不下了,break。否则,在遍历中保存本层的最大高度max_height = max(max_height, books[j - 1][1])。最后,dp[i] = min(dp[i], dp[j - 1] + max_height)—-> 由于当前遍历到的是第j本书,所以需要用到的是前j - 1本书的最小高度dp[j - 1],再加上本层的高度max_height即可(第j本书在本层)。
代码如下:
1 | class Solution { |