题目简介:
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
- 在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。
- 青蛙无法跳回已经访问过的顶点。
- 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
- 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。
无向树的边用数组 edges 描述,其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。
示例 1:
1
2
3
4
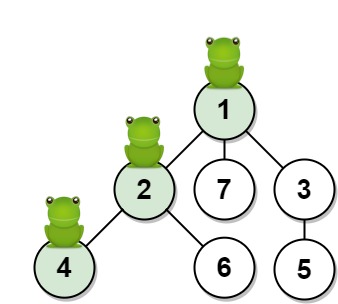
| 输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2,
target = 4
输出:0.16666666666666666
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。
|
提示:
1 <= n <= 100edges.length == n - 1edges[i].length == 21 <= ai, bi <= n1 <= t <= 501 <= target <= n
思路:
深搜,当遍历到一个结点时,如果该结点为target,且t == 0,则说明找到了答案,返回概率1.0。
若t == 0 && now != target,或该结点没有相邻结点了(不能再跳了),则返回概率0.0,即找不到答案。
否则,我们遍历该结点的相邻结点,将各个相邻结点跳到目标结点的概率相加,最后res / nextnode即为当前结点跳到target的最后概率。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
public:
unordered_map<int, int> map;
double solve(vector<vector<int>>& graph, int t, int now, int target){
int next_node = (now == 1) ? graph[now].size() : (graph[now].size() - 1);
if(now == target && t == 0)
return 1.0;
if(now != target && t == 0 || next_node == 0)
return 0.0;
map[now] = 1;
double res = 0;
for(int i = 0; i < graph[now].size(); ++i){
if(map[graph[now][i]] == 0){
res += solve(graph, t - 1, graph[now][i], target);
}
}
return res / next_node;
}
double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
vector<vector<int>> graph(n + 1);
for(auto& edge : edges){
graph[edge[0]].push_back(edge[1]);
graph[edge[1]].push_back(edge[0]);
}
return solve(graph, t, 1, target);
}
};
|
