Keshawn_lu's Blog

吴恩达团队NLP C3_W4_Assignment

吴恩达团队NLP
字数统计: 1.5k阅读时长: 8 min
2021/08/28 Share

吴恩达团队NLP C3_W4_Assignment

任务：判断两个问题是否重复

Part1：数据生成器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
def data_generator(Q1, Q2, batch_size, pad=1, shuffle=True):
    """Generator function that yields batches of data

    Args:
        Q1 (list): List of transformed (to tensor) questions.
        Q2 (list): List of transformed (to tensor) questions.
        batch_size (int): Number of elements per batch.
        pad (int, optional): Pad character from the vocab. Defaults to 1.
        shuffle (bool, optional): If the batches should be randomnized or not. Defaults to True.
    Yields:
        tuple: Of the form (input1, input2) with types (numpy.ndarray, numpy.ndarray)
        NOTE: input1: inputs to your model [q1a, q2a, q3a, ...] i.e. (q1a,q1b) are duplicates
              input2: targets to your model [q1b, q2b,q3b, ...] i.e. (q1a,q2i) i!=a are not duplicates
    """

    input1 = []
    input2 = []
    idx = 0
    len_q = len(Q1)
    question_indexes = [*range(len_q)]
    
    if shuffle:
        rnd.shuffle(question_indexes)
    
    while True:
        if idx >= len_q:
            idx = 0
            if shuffle:
                rnd.shuffle(question_indexes)
        
        q1 = Q1[question_indexes[idx]]
        q2 = Q2[question_indexes[idx]]
        
        idx += 1
        input1.append(q1)
        input2.append(q2)

        if len(input1) == batch_size:
						
		   # 获取问题的最大长度
            max_len = max(max([len(q) for q in input1]), max([len(q) for q in input2]))
            max_len = 2**int(np.ceil(np.log2(max_len)))

            b1 = []
            b2 = []
            for q1, q2 in zip(input1, input2):

                # 填充
                q1 = q1 + [pad] * (max_len - len(q1))
                q2 = q2 + [pad] * (max_len - len(q2))

                b1.append(q1)
                b2.append(q2)

            yield np.array(b1), np.array(b2)

            # reset the batches
            input1, input2 = [], []

test：

1
2
3
4
batch_size = 2
res1, res2 = next(data_generator(train_Q1, train_Q2, batch_size))
print("First questions  : ",'\n', res1, '\n')
print("Second questions : ",'\n', res2)
1
2
3
4
5
6
7
8
9
10
11
First questions  :  
 [[  30   87   78  134 2132 1981   28   78  594   21    1    1    1    1
     1    1]
 [  30   55   78 3541 1460   28   56  253   21    1    1    1    1    1
     1    1]] 

Second questions :  
 [[  30  156   78  134 2132 9508   21    1    1    1    1    1    1    1
     1    1]
 [  30  156   78 3541 1460  131   56  253   21    1    1    1    1    1
     1    1]]

Part2：定义Siamese模型

神经网络结构如下：

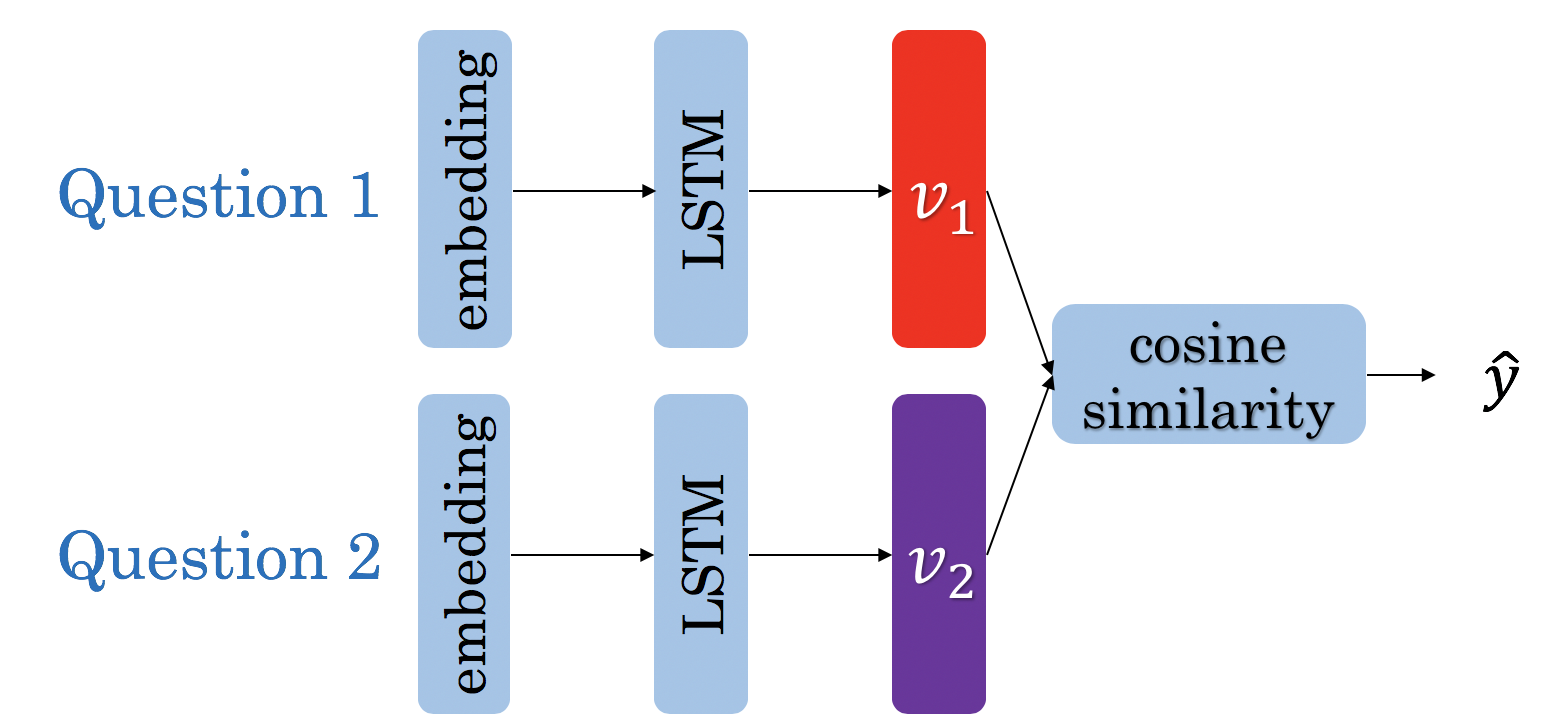
https://pic.imgdb.cn/item/611b5ff34907e2d39c82ff95.png

当我们计算损失函数时，我们使用triplet loss(三元组损失)，如下图所示：

  • 锚示例与正面示例的余弦相似度接近1
  • 锚示例与负面示例的余弦相似度接近-1

https://pic.imgdb.cn/item/611b62a24907e2d39c8d7b50.png

我们需要优化以下公式：

从下图中我们可以看到：

  • 当$cos(A,P) = 1, cos(A,N) = -1$时，成本小于0
  • 反之，则成本大于0

https://pic.imgdb.cn/item/611b63f84907e2d39c9279f1.png

由于我们不想有负成本，所以我们可以用以下公式：

  • 我们使用了α来控制$cos(A,P$)和$cos(A,N)$的距离

通过简化，我们试图最大化以下内容：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def Siamese(vocab_size=len(vocab), d_model=128, mode='train'):
    """Returns a Siamese model.

    Args:
        vocab_size (int, optional): Length of the vocabulary. Defaults to len(vocab).
        d_model (int, optional): Depth of the model. Defaults to 128.
        mode (str, optional): 'train', 'eval' or 'predict', predict mode is for fast inference. Defaults to 'train'.

    Returns:
        trax.layers.combinators.Parallel: A Siamese model. 
    """

    def normalize(x):  # 规范化
        return x / fastnp.sqrt(fastnp.sum(x * x, axis=-1, keepdims=True))
    
    q_processor = tl.Serial(
        tl.Embedding(vocab_size, d_model), # Embedding layer
        tl.LSTM(d_model), # LSTM layer
        tl.Mean(axis = 1), # Mean over columns
        tl.Fn('Normalize', lambda x: normalize(x))  # Apply normalize function
    )  # Returns one vector of shape [batch_size, d_model].
    
    # Run on Q1 and Q2 in parallel.
    model = tl.Parallel(q_processor, q_processor)
    return model

2.1 Hard Negative Mining

我们可以从下图看到，v1,v2只有对应行是重复的(图中数据有误)，所以我们将矩阵相乘。

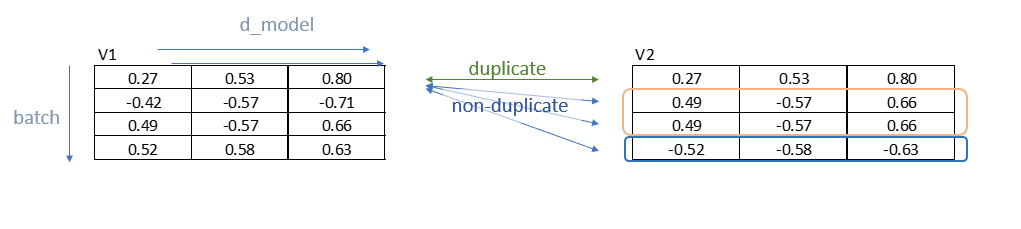
https://pic.imgdb.cn/item/611b67824907e2d39c9fa2a6.png

相乘后，矩阵的对角线便为重复问题的分数，其余为锚点与反面例子的余弦值

https://pic.imgdb.cn/item/611b67c24907e2d39ca08f5f.png

损失函数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def TripletLossFn(v1, v2, margin=0.25):
    """Custom Loss function.

    Args:
        v1 (numpy.ndarray): Array with dimension (batch_size, model_dimension) associated to Q1.
        v2 (numpy.ndarray): Array with dimension (batch_size, model_dimension) associated to Q2.
        margin (float, optional): Desired margin. Defaults to 0.25.

    Returns:
        jax.interpreters.xla.DeviceArray: Triplet Loss.
    """
    
	# 矩阵相乘
    scores = fastnp.dot(v1, v2.T)
    
    batch_size = len(scores)
    
    # 获取对角线的值
    positive = fastnp.diagonal(scores)  
    
    # eye() 生成对角线矩阵，对角线处为1，其余为0
    negative_without_positive = scores - 2.0 * fastnp.eye(batch_size)  
    
    # 除去对角线值外的每行最大值  
    closest_negative = negative_without_positive.max(axis = 1)
    
    # 使得scores矩阵对角线处为0，其余不变
    negative_zero_on_duplicate = scores * (1.0 - fastnp.eye(batch_size))
    
    # 求每行平均值 
    mean_negative =fastnp.sum(negative_zero_on_duplicate, axis=1) / (batch_size - 1)
     
    triplet_loss1 = fastnp.maximum(0.0, margin - positive + closest_negative)
   
    triplet_loss2 = fastnp.maximum(0.0, margin - positive + mean_negative)

    triplet_loss = fastnp.mean(triplet_loss1 + triplet_loss2)
    
    return triplet_loss

2.2 编写没有可训练变量的损失层

1
2
3
4
from functools import partial
def TripletLoss(margin=0.25):
    triplet_loss_fn = partial(TripletLossFn, margin=margin)
    return tl.Fn('TripletLoss', triplet_loss_fn)

Part3：训练模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
lr_schedule = trax.lr.warmup_and_rsqrt_decay(400, 0.01)

def train_model(Siamese, TripletLoss, lr_schedule, train_generator=train_generator, val_generator=val_generator, output_dir='model/'):
    """Training the Siamese Model

    Args:
        Siamese (function): Function that returns the Siamese model.
        TripletLoss (function): Function that defines the TripletLoss loss function.
        lr_schedule (function): Trax multifactor schedule function.
        train_generator (generator, optional): Training generator. Defaults to train_generator.
        val_generator (generator, optional): Validation generator. Defaults to val_generator.
        output_dir (str, optional): Path to save model to. Defaults to 'model/'.

    Returns:
        trax.supervised.training.Loop: Training loop for the model.
    """
    output_dir = os.path.expanduser(output_dir)

    train_task = training.TrainTask(
        labeled_data=train_generator, 
        loss_layer=TripletLoss(), # 损失函数
        optimizer=trax.optimizers.Adam(0.01),
        lr_schedule=lr_schedule, 
    )

    eval_task = training.EvalTask(
        labeled_data=val_generator,
        metrics=[TripletLoss()], 
    )

    training_loop = training.Loop(Siamese(),
                                  train_task,
                                  eval_tasks=eval_task,
                                  output_dir=output_dir)

    return training_loop

Part4：评估模型

4.1 导入之前训练的模型

1
2
model = Siamese()
model.init_from_file('model.pkl.gz')

4.2 分类测试准确率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def classify(test_Q1, test_Q2, y, threshold, model, vocab, data_generator=data_generator, batch_size=64):
    """Function to test the accuracy of the model.

    Args:
        test_Q1 (numpy.ndarray): Array of Q1 questions.
        test_Q2 (numpy.ndarray): Array of Q2 questions.
        y (numpy.ndarray): Array of actual target.
        threshold (float): Desired threshold.
        model (trax.layers.combinators.Parallel): The Siamese model.
        vocab (collections.defaultdict): The vocabulary used.
        data_generator (function): Data generator function. Defaults to data_generator.
        batch_size (int, optional): Size of the batches. Defaults to 64.

    Returns:
        float: Accuracy of the model.
    """
    accuracy = 0

    for i in range(0, len(test_Q1), batch_size):
        q1, q2 = next(data_generator(test_Q1[i:i + batch_size], test_Q2[i:i + batch_size], batch_size, vocab['<PAD>'], shuffle=False))
        
        y_test = y[i:i + batch_size]

        v1, v2 = model((q1, q2))

        for j in range(batch_size):
            d = np.dot(v1[j], v2[j].T)

            # 判断是否大于阈值
            res = d > threshold
            accuracy += (y_test[j] == res)
            
    accuracy = accuracy / len(test_Q1)
    
    return accuracy

Part5：测试自己的问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def predict(question1, question2, threshold, model, vocab, data_generator=data_generator, verbose=False):
    """Function for predicting if two questions are duplicates.

    Args:
        question1 (str): First question.
        question2 (str): Second question.
        threshold (float): Desired threshold.
        model (trax.layers.combinators.Parallel): The Siamese model.
        vocab (collections.defaultdict): The vocabulary used.
        data_generator (function): Data generator function. Defaults to data_generator.
        verbose (bool, optional): If the results should be printed out. Defaults to False.

    Returns:
        bool: True if the questions are duplicates, False otherwise.
    """

	# 变成单词列表
    q1 = nltk.word_tokenize(question1)
    q2 = nltk.word_tokenize(question2)
    Q1, Q2 = [], []

    for word in q1:
        Q1 += [vocab[word]]
    for word in q2:
        Q2 += [vocab[word]]
        
    # print(Q1)
      
    Q1, Q2 = next(data_generator([Q1], [Q2], 1, vocab['<PAD>']))
    v1, v2 = model((Q1, Q2))
    
    # print(v1, v2)
    
    d = np.dot(v1[0], v2[0].T)
    res = d > threshold
    
    if(verbose):
        print("Q1  = ", Q1, "\nQ2  = ", Q2)
        print("d   = ", d)
        print("res = ", res)

    return res

test：

1
2
3
4
question1 = "When will I see you?"
question2 = "When can I see you again?"
# 1 means it is duplicated, 0 otherwise
predict(question1 , question2, 0.7, model, vocab, verbose = True)
1
2
3
4
Q1  =  [[585  76   4  46  53  21   1   1]] 
Q2  =  [[ 585   33    4   46   53 7280   21    1]]
d   =  0.88113236
res =  True
CATALOG
  1. 1. 吴恩达团队NLP C3_W4_Assignment
    1. 1.1. 任务：判断两个问题是否重复
    2. 1.2. Part1：数据生成器
      1. 1.2.1. test：
    3. 1.3. Part2：定义Siamese模型
      1. 1.3.1. 2.1 Hard Negative Mining
      2. 1.3.2. 2.2 编写没有可训练变量的损失层
    4. 1.4. Part3：训练模型
    5. 1.5. Part4：评估模型
      1. 1.5.1. 4.1 导入之前训练的模型
      2. 1.5.2. 4.2 分类测试准确率
    6. 1.6. Part5：测试自己的问题
      1. 1.6.1. test：
Total : 424
2023
2022
2021
2020
2019
动态规划 树 深度优先搜索 哈希表 数组 深度优先遍历 单调栈 字符串 双指针 栈 贪心 图 模拟 广度优先搜索 回溯 滑动窗口 二分查找 广度优先遍历 记忆化搜索 数学 链表 前缀和 双向链表 优先队列 拓扑排序 KMP 堆 字典树 递归 并查集 矩阵 位运算 双端队列 吴恩达团队NLP 吴恩达深度学习 线性表
杂谈 算法相关 PAT 2019推理小说阅读计划 NLP 深度学习 大三课程学习 大四课程学习 浙工商OJ 牛客网